Hashes: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
| (30 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
*Da die Menge der möglichen Hashwerte meist kleiner ist als die der möglichen Eingaben, sind solche Kollisionen dann prinzipiell unvermeidlich. | *Da die Menge der möglichen Hashwerte meist kleiner ist als die der möglichen Eingaben, sind solche Kollisionen dann prinzipiell unvermeidlich. | ||
*Eine gute Hashfunktion zeichnet sich dadurch aus, dass sie für die Eingaben, für die sie entworfen wurde, möglichst wenige Kollisionen erzeugt. | *Eine gute Hashfunktion zeichnet sich dadurch aus, dass sie für die Eingaben, für die sie entworfen wurde, möglichst wenige Kollisionen erzeugt. | ||
| + | =Funktion= | ||
| + | ;Auf Rechner1 wird aus den Daten ein Hash-Rechner1 gebildet | ||
| + | {{#drawio:hash}} | ||
| + | |||
| + | |||
| + | ;Rechner1 schickt Daten und Hash an Rechner2 | ||
| + | {{#drawio:r1-r2}} | ||
| + | |||
| + | |||
| + | ;Rechner2 bidet aus den empfangenen Daten den Hash-Rechner2 | ||
| + | {{#drawio:hash-r2}} | ||
| + | |||
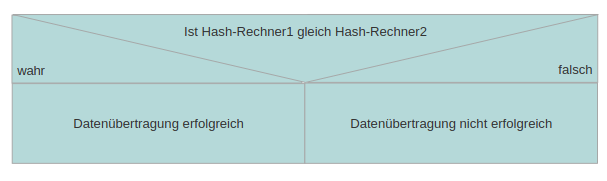
| + | ;Ergebnis | ||
| + | |||
| + | [[Datei:Hash-ergebnis.png]] | ||
=Anwendungen= | =Anwendungen= | ||
| Zeile 17: | Zeile 32: | ||
*Kryptologie | *Kryptologie | ||
**In der Kryptologie werden spezielle kryptologische Hashfunktionen verwendet, bei denen zusätzlich gefordert wird, dass es praktisch unmöglich ist, Kollisionen absichtlich zu finden. | **In der Kryptologie werden spezielle kryptologische Hashfunktionen verwendet, bei denen zusätzlich gefordert wird, dass es praktisch unmöglich ist, Kollisionen absichtlich zu finden. | ||
| + | |||
=Kryptologische Hashfunktionen= | =Kryptologische Hashfunktionen= | ||
*Eine kryptologische Hashfunktion oder kryptographische Hashfunktion ist eine spezielle Form der Hashfunktion, welche kollisionsresistent sein sollte und nach Definition immer eine Einwegfunktion ist. | *Eine kryptologische Hashfunktion oder kryptographische Hashfunktion ist eine spezielle Form der Hashfunktion, welche kollisionsresistent sein sollte und nach Definition immer eine Einwegfunktion ist. | ||
| − | *Kryptologische Hashfunktionen werden in schlüssellose und schlüsselabhängige eingeteilt. | + | *Kryptologische Hashfunktionen werden in schlüssellose und schlüsselabhängige eingeteilt. |
| − | * | + | =Einfaches Beispiel Quersumme= |
| − | * | + | *Fritz bekommt als Rechnaufgabe auf <math>x</math> auszurechnen. <math>x = 9^2\times 2+7</math> |
| + | *Die Quersumme beträgt 16. | ||
| + | *Fritz rechnet aus 169 aus. | ||
| + | *Fritz zählt <math>1+6+9=16</math> | ||
| + | *Ergebnis stimmt. | ||
=Merkle-Damgård-Verfahren= | =Merkle-Damgård-Verfahren= | ||
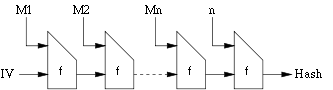
| − | *Bei der Merkle-Damgård-Konstruktion wird die eingegebene Nachricht M zuerst in Blöcke fester Länge geteilt | + | *Bei der Merkle-Damgård-Konstruktion wird die eingegebene Nachricht M zuerst in Blöcke fester Länge geteilt |
| − | *Die Funktion hat als Input einen Nachrichtenblock und den Output der | + | *Der letzte Block wird mit zusätzlichen Bits aufgefüllt, so dass die Eingabelänge ein ganzzahliges Vielfaches der Blocklänge beträgt. |
| + | *Die Funktion hat als Input einen Nachrichtenblock und den Wert des letzten Hashberechnung(ausser beim ersten Block). | ||
| + | *Der Output entspricht dem Wert der neuen Hashberechnung. | ||
*Der Hashwert der gesamten Nachricht ist der Hashwert des letzten Blocks: | *Der Hashwert der gesamten Nachricht ist der Hashwert des letzten Blocks: | ||
| − | |||
| − | |||
: <math>\begin{align} | : <math>\begin{align} | ||
| Zeile 34: | Zeile 54: | ||
h\left(M \right) & = H(t) | h\left(M \right) & = H(t) | ||
\end{align}</math> | \end{align}</math> | ||
| − | IV bezeichnet einen Startwert (initial value). | + | IV bezeichnet einen festen Startwert (initial value). |
Aktuelle Version vom 15. Juni 2021, 16:41 Uhr
Grundlagen
Hashfunktion
- Eine Hashfunktion (auch Streuwertfunktion) ist eine Abbildung, die eine große Eingabemenge (die Schlüssel) auf eine kleinere Zielmenge (die Hashwerte) abbildet.
- Eine „gute“ Hashfunktion liefert dabei für die (erwarteten) Eingabedaten Werte so, dass zwei unterschiedliche Eingaben auch zu unterschiedlichen Ausgabewerten führen.
- Ein Hashwert wird deshalb auch als englisch Fingerprint bezeichnet, da er eine nahezu eindeutige Kennzeichnung einer größeren Datenmenge darstellt.
Kollisionen
- Eine sog. Kollision tritt dann auf, wenn unterschiedlichen Eingabedaten derselbe Hashwert zugeordnet wird.
- Da die Menge der möglichen Hashwerte meist kleiner ist als die der möglichen Eingaben, sind solche Kollisionen dann prinzipiell unvermeidlich.
- Eine gute Hashfunktion zeichnet sich dadurch aus, dass sie für die Eingaben, für die sie entworfen wurde, möglichst wenige Kollisionen erzeugt.
Funktion
- Auf Rechner1 wird aus den Daten ein Hash-Rechner1 gebildet
- Rechner1 schickt Daten und Hash an Rechner2
- Rechner2 bidet aus den empfangenen Daten den Hash-Rechner2
- Ergebnis
Anwendungen
Hashfunktionen haben verschiedene Anwendungsfelder. Dabei lassen sich drei große Gebiete unterteilen:
- Datenbanken
- In der Datenspeicherung kann ein Hashwert verwendet werden, um die Speicherstelle der angefragten Daten zu berechnen (z. B. Hashtabelle).
- Prüfsummen
- Bei Prüfsummen verwendet man Hashwerte, um Übertragungsfehler zu erkennen.
- Kryptologie
- In der Kryptologie werden spezielle kryptologische Hashfunktionen verwendet, bei denen zusätzlich gefordert wird, dass es praktisch unmöglich ist, Kollisionen absichtlich zu finden.
Kryptologische Hashfunktionen
- Eine kryptologische Hashfunktion oder kryptographische Hashfunktion ist eine spezielle Form der Hashfunktion, welche kollisionsresistent sein sollte und nach Definition immer eine Einwegfunktion ist.
- Kryptologische Hashfunktionen werden in schlüssellose und schlüsselabhängige eingeteilt.
Einfaches Beispiel Quersumme
- Fritz bekommt als Rechnaufgabe auf auszurechnen.
- Die Quersumme beträgt 16.
- Fritz rechnet aus 169 aus.
- Fritz zählt
- Ergebnis stimmt.
Merkle-Damgård-Verfahren
- Bei der Merkle-Damgård-Konstruktion wird die eingegebene Nachricht M zuerst in Blöcke fester Länge geteilt
- Der letzte Block wird mit zusätzlichen Bits aufgefüllt, so dass die Eingabelänge ein ganzzahliges Vielfaches der Blocklänge beträgt.
- Die Funktion hat als Input einen Nachrichtenblock und den Wert des letzten Hashberechnung(ausser beim ersten Block).
- Der Output entspricht dem Wert der neuen Hashberechnung.
- Der Hashwert der gesamten Nachricht ist der Hashwert des letzten Blocks:
IV bezeichnet einen festen Startwert (initial value).